Analytic geometry is defined by one or more boolean functions of x, y and z in the spatial domain. The Analytic Geometry Editor, accessible from the geometry view of a BioModel application or MathModel, provides an interface for entering 1, 2, or 3 dimensional boolean functions.

Create a new analytic geometry within an application from the Geometry tab of the view Panel. Select the "Geometry Definition" view and select "Add/Replace Geometry"->New. and from the popup window choose Analytic Equations (1D,2D,3D). The view will switch to the Analytic Geometry editor.
Define overall boundaries (origin and size) of the geometry by selecting the "Edit Domain..." button and filling in the size of the domain and the position of the origion within the domain. The default geometry has a single subdomain (subdomain0) that encompass the entire geometry.
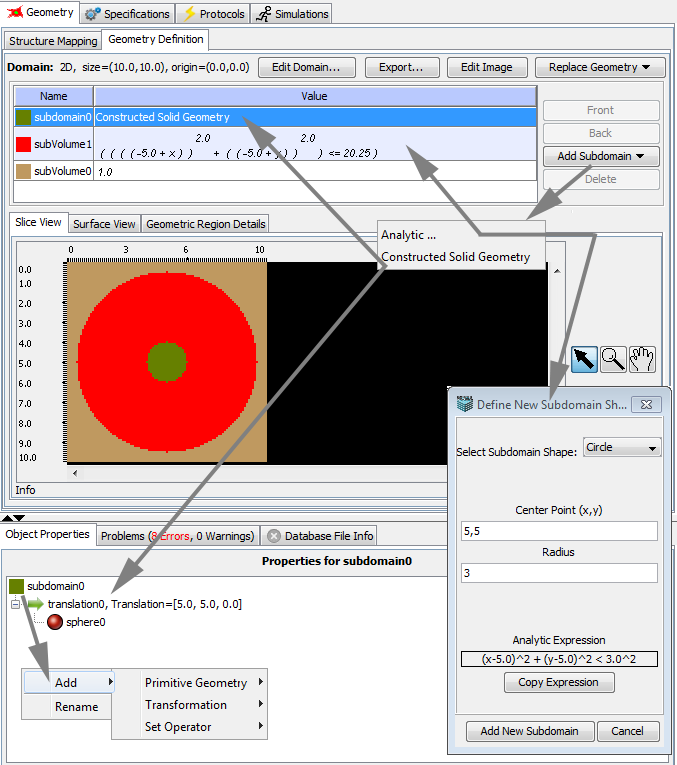
Create a new domain based on an analytic function by clicking the Add Subdomain… button. Choose the Analytic... menu item to show the analytic function helper. A function defines all the points within the geometry boundary where a subdomain is to be assigned. Simple definitions are provided for commonly used analytic function shapes or functions can be entered completely manually. The simple definitions (e.g. circle) can be used as is or are useful as templates for more complicated shapes. Simple definitions require the user to enter only a few parameters (e.g. center and radius) that define a particular shape. Subdomains can also be added as CSG definitions by choosing the Constructive Solid Geometry menu item. The object properties panel below the subdomain table will show a new CSG subdomain that is editable. Right-click to rename the subdomain if necessary. Construct a subdomain using CSG by adding 1 or more geometric primitives(rt-click object properties csg domain->add->primitive geometry). Adjust the size(scale) and position(translation) of each added primitive in relation to one another as well as the rules for combining primitives into a final subdomain definition. For example, to define a sphere (or 2D circle) csg, rt-click object property csg subdomain->add->Primitive Geometry->sphere, a new 'sphere' (or 2D circle) will appear at coordinates(x,y,z) 0,0,0 in your geometry domain. Select the new 'sphere' from the tree view and rt-click->Transform->translation to reposition the object within your domain, you will see a new 'translation' object is now above the 'sphere' object in the tree view. Select the 'translation' object and rt-click->edit to change the position (translation) of the sphere and any other primitives you may add later. CSG primitives can be combined using union and intersection rules to create more intricate subdomain definitions.
Re-Order the list of subdomains by selecting a specific subdomain and pressing the front or back buttons. A new subdomain is placed at the top of the subdomain table list.
The final geometry is created from the subdomain list by evaluating each function at values of x, y, z starting at the bottom of the list. Non-zero function values at a particular x, y, z coordinate mark a point in the geometry as being part of that function's subdomain. Non-zero subdomain values that come from functions higher in the table list functions replace any previous subdomain values as the evaluation proceeds. A display of the overall geometry defined by the current set of subdomain functions is displayed below the table list.
Edit analytic functions within the geometry definition tab if the current model geometry is already an analytic type.